
A z-score table identifies the probability of obtaining a value LESS THAN a certain z-score, or to the left of the value when visually observing a normal distribution.
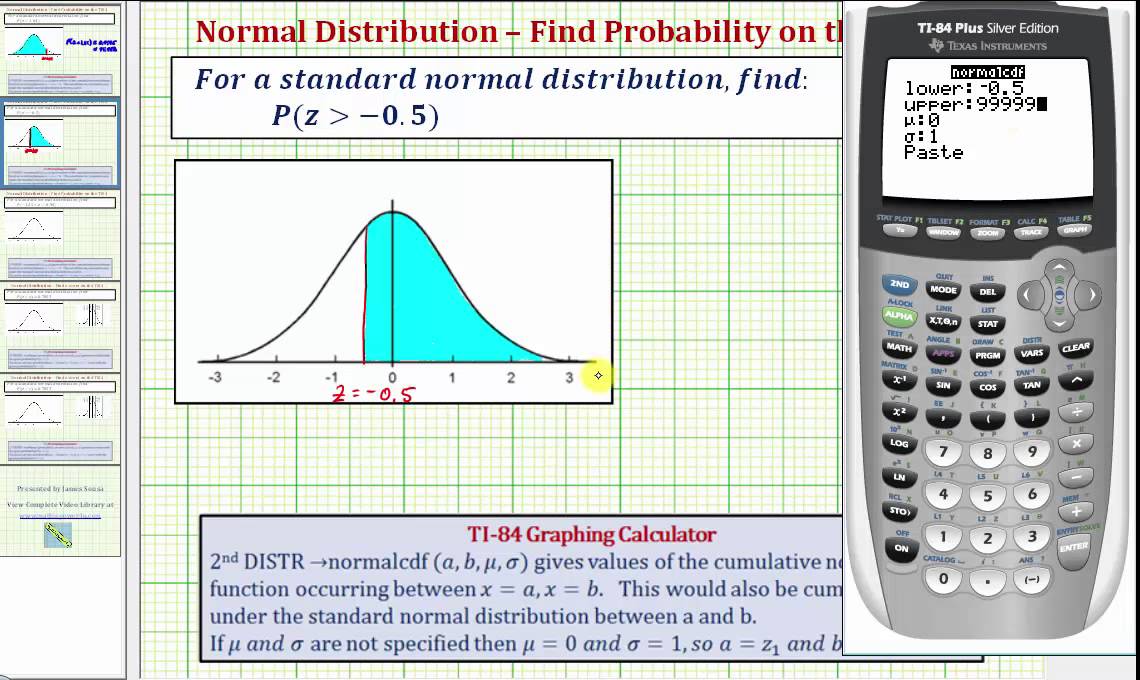
To find these probabilities, it is possible to use a z-score table. Or, it is even possible to identify the likelihood of obtaining a value between one standard deviation below and two standard deviations above the mean. Or, they might want to find the likelihood of obtaining a value that is two standard deviations above the mean.

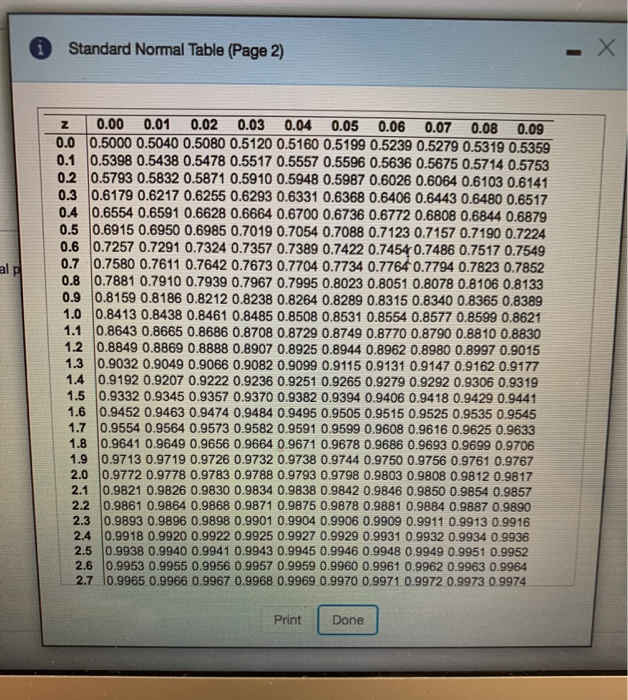
For example, someone may want to find the likelihood of obtaining a value that is one standard deviation less than the mean. These can be found in the back of most introductory statistics textbooks or performing a simple google search for a “z-value table.” If you have any questions or comments about this guide, please email me at researchers and practitioners want to identify the probability of obtaining a certain value while assuming a normal distribution in their data. This guide requires the use of a z-value table. What is the probability that a male aged 60 has BMI between 30 and 35? Note that this is the same as asking what proportion of men aged 60 have BMI between 30 and 35.The current page provides a guide on finding the probability associated with certain z-value ranges when assuming a normal distribution. Or, we can use R to compute the entire thing in a single step as follows: So the probability of a 60 year ld man having a BMI greater than 35 is 15.8%. What is the probability that a 60 year old man will have a BMI greater than 35?ģ5-29=6, which is one standard deviation above the mean. What is the probability that a 60 year old man will have a BMI less than 30? The Z-score was 0.16667. What is the probability that a 60 year old man in the population above has a BMI less than 29 (the mean)? The Z-score would be 0, and pnorm(0)=0.5 or 50%. For example,Ī Z-score of 0 (the mean of any distribution) has 50% of the area to the left. Normal Probability CalculatorĪs an alternative to looking up normal probabilities in the table or using Excel, we can use R to compute probabilities. Interpretation: Almost 16% of men aged 60 have BMI over 35. We now go to the standard normal distribution table to look up P(Z>1) and for Z=1.00 we find that P(Z1)=1-0.8413=0.1587. The units place and the first decimal place are shown in the left hand column, and the second decimal place is displayed across the top row.īut let's get back to the question about the probability that the BMI is less than 30, i.e., P(X 35)? Again we standardize: Note also that the table shows probabilities to two decimal places of Z. In this case, because the mean is zero and the standard deviation is 1, the Z value is the number of standard deviation units away from the mean, and the area is the probability of observing a value less than that particular Z value. This table is organized to provide the area under the curve to the left of or less of a specified value or "Z value". Probabilities of the Standard Normal Distribution Z
#How to find z score on standard normal table plus#
So, the 50% below the mean plus the 34% above the mean gives us 84%. That is because one standard deviation above and below the mean encompasses about 68% of the area, so one standard deviation above the mean represents half of that of 34%. The table in the frame below shows the probabilities for the standard normal distribution. Examine the table and note that a "Z" score of 0.0 lists a probability of 0.50 or 50%, and a "Z" score of 1, meaning one standard deviation above the mean, lists a probability of 0.8413 or 84%. For any given Z-score we can compute the area under the curve to the left of that Z-score. Since the area under the standard curve = 1, we can begin to more precisely define the probabilities of specific observation. After standarization, the BMI=30 discussed on the previous page is shown below lying 0.16667 units above the mean of 0 on the standard normal distribution on the right. However, when using a standard normal distribution, we will use "Z" to refer to a variable in the context of a standard normal distribution. To this point, we have been using "X" to denote the variable of interest (e.g., X=BMI, X=height, X=weight). For the standard normal distribution, 68% of the observations lie within 1 standard deviation of the mean 95% lie within two standard deviation of the mean and 99.9% lie within 3 standard deviations of the mean. The standard normal distribution is centered at zero and the degree to which a given measurement deviates from the mean is given by the standard deviation. The standard normal distribution is a normal distribution with a mean of zero and standard deviation of 1.


 0 kommentar(er)
0 kommentar(er)
